

Problém směrování vozidel s více sklady
Taxonomické označení: MDVRP
U této varianty je nutné při hledání optimálního řešení problému brát v úvahu dodávky z více skladů.
Při řešení se opět minimalizují celkové náklady na trasu.
Základem je optimální alokace zákazníků do jednotlivých skladů dle jejich požadavku. Nesmí být překročena kapacita skladů a je stanoveno pořadí, ve kterém jsou zákazníci obslouženi.
K popisu matematického modelu je nutné definovat pojmy, které objasňují rozdíly oproti klasickému VRP. Hlavní rozdíl mezi depem a skladem spočívá v tom, že vozidla musí svou trasu zahájit a ukončit v depu.
Zajímavosti
Řešení tohoto problému vyžaduje nejen optimalizaci tras vozidel, ale také efektivní alokaci zákazníků k jednotlivým skladům. Zajímavé je, že některé moderní logistické systémy dokážou dynamicky přesměrovávat vozidla mezi sklady podle aktuální dostupnosti zboží, čímž minimalizují časy dodání a zlepšují využití skladových zásob.
- Rozdělení zákaznické oblasti
- Rovnováha zatížení skladů
- Heterogenní flotila napříč sklady
- Možnost přechodů mezi sklady
- Význam pro distribuční sítě ve více regionech
Praktické využití
MDVRP se uplatňuje například v e-commerce, kde velké distribuční společnosti, jako Amazon nebo DHL, optimalizují dodávky z více logistických center. Dalším příkladem je zásobování čerpacích stanic palivem, kdy se zboží dováží z několika rafinerií nebo centrálních skladů tak, aby bylo zajištěno pravidelné a efektivní doplňování zásob.
- Nápojové společnosti s regionálními sklady
- Servis klimatizací a topení
- Zásobování maloobchodních sítí
- E-commerce vyzvedávání vratných obalů
- Doručování zdravotnického materiálu
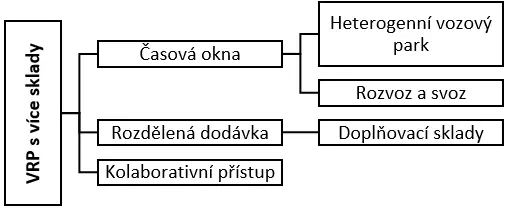
Metody řešení




Shrnutí
Problém směrování vozidel s více sklady (MDVRP) řeší optimální rozdělení zákazníků mezi sklady a plánování tras tak, aby se minimalizovaly náklady a dojezdové vzdálenosti. Tento model je klíčový pro efektivní logistiku, zejména v distribuci zboží, dodávkách paliva nebo v e-commerce, kde umožňuje rychlejší a levnější dodání objednávek.
Zdroj:
[1] Laporte, G., Mercure, H., & Nobert, Y. (1986). An exact algorithm for the asymmetrical capacitated vehicle routing problem. Networks, 16(1).
[2] Zhou, L., Baldacci, R., Vigo, D., Wand, X. (2018). A Multi-Depot Two-Echelon Vehicle Routing Problem with Delivery Options Arising in the Last Mile Distribution. European Journal of Operational Research, 265.
[3] Alinaghian, M., Shokouhi, N. (2018). Multi-depot multi-compartment vehicle routing problem, solved by a hybrid adaptive large neighborhood search. Omega, 76.
[4] Kulkarni, R. V., & Bhave, P. R. (1985). Integer programming formulations of vehicle routing problems. European journal of operational research, 20(1).
[5] Nagy, G., & Salhi, S. (2005). Heuristic algorithms for single and multiple depot vehicle routing problems with pickups and deliveries. European journal of operational research, 162(1).
[6] Pajonk, T. Modifikace rozvozního problému [online]. Praha, 2007 [cit. 2021-02-15]. Dostupné z: https://www.vse.cz/vskp/id/14317
Důležité odkazy
Kontakt
List Title
- kvetapapouskova@gmail.com
- Univerzitní 22, 306 14 Plzeň