
Úloha s více vozidly
Úloha s více vozidly je logickým rozšířením dynamické úlohy, které nabízí navýšení omezené kapacity jednoho vozidla o kapacitu vozidla dalšího. Dochází k minimalizaci času čekání zákazníka na obsloužení pouze jedním vozidlem. Předpokladem je neomezený počet vozidel ve výchozím místě a primárním cílem se stává přijmout co největší počet požadavků. Této problematice se věnuje řada prací (Bertsimas & van Ryzin, 1991; 1993; Gendreau a kol., 1999; Attanasio a kol., 2004; Haghani & Jung, 2005; Potvin & Benyahia, 2006).
Zajímavost
Koordinace mezi více vozidly ztěžuju dynamiku plánování, protože je třeba zohlednit dostupnost jednotlivých řidičů.
Praktické využití
Sdílené taxi služby, systémy carpoolingu a logistika e-commerce.
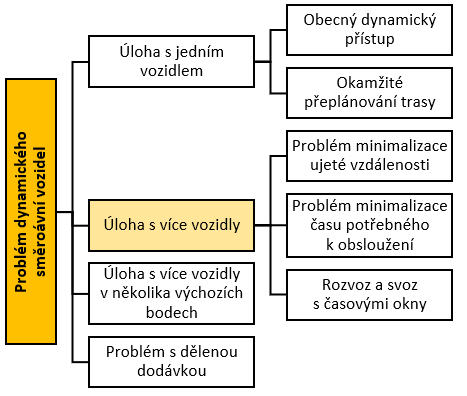
Tuto variantu DVRP je možné najít ve třech modifikacích:
Metody řešení
Tento model zahrnuje optimalizaci tras pro více vozidel tak, aby se dosáhlo co nejefektivnějšího výkonu v závislosti na různých kritériích (vzdálenost, čas, kapacita).
Zdroj:
[1] Bertsimas, D. J., & Van Ryzin, G. (1991). A stochastic and dynamic vehicle routing problem in the Euclidean plane. Operations Research, 39(4).
[2] Bertsimas, D. J., & Van Ryzin, G. (1993). Stochastic and dynamic vehicle routing in the Euclidean plane with multiple capacitated vehicles. Operations Research, 41(1).
[3] Gendreau, M., Guertin, F., Potvin, J. Y., & Taillard, É. (1999). Parallel tabu search for real-time vehicle routing and dispatching. Transportation science, 33(4).
[4] Attanasio, A., Cordeau, J. F., Ghiani, G., & Laporte, G. (2004). Parallel tabu search heuristics for the dynamic multi-vehicle dial-a-ride problem. Parallel Computing, 30(3).
[5] Haghani, A., & Jung, S. (2005). A dynamic vehicle routing problem with time-dependent travel times. Computers & operations research, 32(11).
[6] Potvin, J. Y., Xu, Y., & Benyahia, I. (2006). Vehicle routing and scheduling with dynamic travel times. Computers & Operations Research, 33(4).