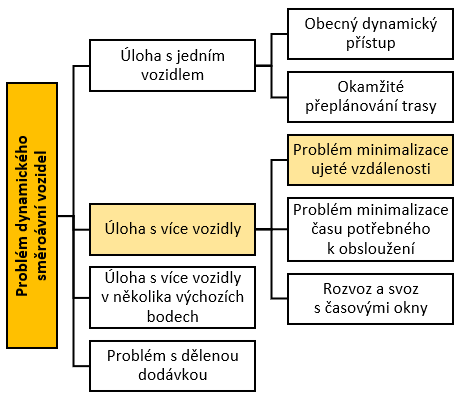
Minimalizace ujeté vzdálenosti

Úloha s více vozidly je logickým rozšířením předchozí úlohy, které nabízí navýšení omezené kapacity jednoho vozidla o kapacitu vozidla dalšího. Dochází k minimalizaci času čekání zákazníka na obsloužení pouze jedním vozidlem. Předpokladem je neomezený počet vozidel ve výchozím místě a primárním cílem se stává přijmout co největší počet požadavků a minimem ujeté vzdálenosti.

Zajímavost

Minimalizace vzdálenosti šetří palivo a snižuje emise.

Praktické využití

• Tento přístup je častý v praxi městské logistiky, distribuce zboží s vysokou frekvencí objednávek, nebo při expresním rozvozu, kde je klíčové snížit nejen čekací dobu, ale i náklady.
• Ekologická logistika a udržitelné doručování.

Dynamický problém směrování s více vozidly zaměřený na minimalizaci ujeté vzdálenosti klade důraz na optimalizaci celkové délky tras všech vozidel v systému. Cílem je snížit provozní náklady a environmentální dopady, přičemž systém reaguje na příchod požadavků v reálném čase a okamžitě přepočítává trasy.

Zdroj:
[1] Bertsimas, D. J., & Van Ryzin, G. (1991). A stochastic and dynamic vehicle routing problem in the Euclidean plane. Operations Research, 39(4).
[2] Bertsimas, D. J., & Van Ryzin, G. (1993). Stochastic and dynamic vehicle routing in the Euclidean plane with multiple capacitated vehicles. Operations Research, 41(1).
[3] Gendreau, M., Guertin, F., Potvin, J. Y., & Taillard, É. (1999). Parallel tabu search for real-time vehicle routing and dispatching. Transportation science, 33(4).
[4] Attanasio, A., Cordeau, J. F., Ghiani, G., & Laporte, G. (2004). Parallel tabu search heuristics for the dynamic multi-vehicle dial-a-ride problem. Parallel Computing, 30(3).
[5] Haghani, A., & Jung, S. (2005). A dynamic vehicle routing problem with time-dependent travel times. Computers & operations research, 32(11).
[6] Potvin, J. Y., Xu, Y., & Benyahia, I. (2006). Vehicle routing and scheduling with dynamic travel times. Computers & Operations Research, 33(4).