Kapacitní okružní dopravní problém
Taxonomické označení: CVRP
Zboží dodávané zákazníkovi je limitováno pouze jednou proměnnou a tou je maximální disponibilní kapacita vozidel. Zabývá se stanovením souboru tras, které vykazují nejnižší náklady, za předpokladu obsloužení zákazníka pouze jednou trasou a jedním vozidlem tak, aby nedošlo k překročení jeho nosnosti.
Hlavním úkolem je nalézt soubor dopravních cest (tras) s nejnižšími náklady (což je zaručeno v případě, že se jedná o jednu trasu pro každé vozidlo) aniž by:
- došlo k překročení únosnosti (kapacity) vozidel,
- počátek a konec cesty je v základním depu a
- každý zákazník je obsloužen pouze jedním vozidlem.
Zajímavosti
Kapacitní rozvozní problém (CVRP) se v praxi využívá například při zásobování supermarketů, kde je třeba optimálně naplánovat trasy nákladních vozů s omezenou kapacitou tak, aby efektivně rozvezly zboží do několika poboček a minimalizovaly náklady na dopravu.
Další možností využití CVRP je kupříkladu při plánování tras pro mobilní krevní banky, kde musí sanitky s omezenou kapacitou navštívit co nejvíce dárcovských míst a zároveň udržet krev v optimálních podmínkách.
Shrnutí
V tomto projektu jsou jednotlivé typy VRP posuzovány jako problémy vycházející z myšlenky CVRP, ale je jim dále věnován vlastní prostor pro další členění.
Toto výsadní postavení získávají právě díky zpřesnění matematického modelu o významné omezující podmínky nebo definování klíčového parametru.
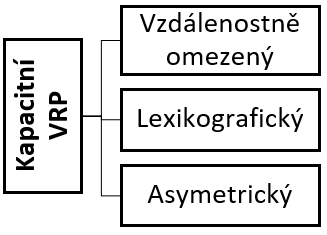
Členění kapacitního okružního problému je na uvedeném schématu.
Zdroj:
[1] Toth, P., Vigo, D. (1997). An exact algorithm for the vehicle routing problem with backhauls. Transportation Science, 31(4).
[2] Beardwood, J., Halton, J. Hammersley, J. (1959). The shortest path through many points. Mathematical Proceeeding of the Cambridge Philosophical Society, 55(4).
[3] Wilson, H., Weissberg, H. (1967). Advandced dial-a-ride algorithms research project: Final report. Technical Report.
[4] Gutiérrez-Sánchez, A., Rocha-Medina, L. B. (2022). VRP variants applicable to collecting donations and similar problems: A taxonomic review. Computers & Industrial Engineering,164.
[5] Gribkovskaia, I., & Laporte, G. (2008). One-to-many-to-one single vehicle pickup and delivery problems. In The Vehicle Routing Problem: Latest Advances and New Challenges (pp. 359-377). Springer, Boston, MA.
[6] Min, H. (1989). The multiple vehicle routing problem with simultaneous delivery and pick-up points.
Trans. Res. A Gen. 23.