Manage and streamline operations across multiple locations, sales channels, and employees to has improve efficiency and your bottom line.

Problémy se stochastickou přítomností zákazníků a stochastickou poptávkou s Poissonovo rozdělením

Jedná se o problémy se stochastickou přítomností zákazníků.

Stochastická poptávka – Poissonovo rozdělení

CVRPSCD (Capacitated Vehicle Routing Problem with Stochastic Customer Demand) řeší situaci, kdy není jisté, zda zákazníci budou potřebovat obsluhu. To znamená, že trasu je nutné plánovat s ohledem na pravděpodobnost, že určitý zákazník bude aktivní. Tento problém je běžný v dodávkových a svozových službách, kde objednávky přicházejí náhodně.

Problémy se stochastickou přítomností zákazníků a stochastickou poptávkou s Poissonovým rozdělením představují komplexní variantu logistických problémů, kde je nejen náhodná přítomnost zákazníků, ale i poptávka po službách či produktech, která se řídí Poissonovým rozdělením. Tento model je ideální pro situace, kdy poptávka je spojena s náhodnými, ale vzorcovitými událostmi, jako jsou například poruchy nebo požadavky na údržbu, které se vyskytují podle náhodného procesu. Poissonovo rozdělení je běžně používáno pro modelování událostí, které se vyskytují nezávisle a s konstantní průměrnou frekvencí, což je častý scénář například ve správě infrastruktury, poštovních službách nebo v distribuci.

Zajímavost

  • Poissonovo rozdělení poptávky: Tento typ stochastické poptávky je velmi užitečný pro modelování situací, kde se požadavky vyskytují v určitém časovém okně nebo prostoru, ale jejich výskyt je náhodný. Například v případě údržby energetických sítí nebo opravy vozidel mohou být požadavky na opravy modelovány pomocí Poissonova rozdělení, kde počet poruch v daném časovém období je náhodný, ale má stanovenou průměrnou frekvenci.
  • Stochastická přítomnost zákazníků: Zákazníci nemusí být vždy dostupní pro službu, což vytváří další úroveň komplexity pro trasování a distribuci. Počet zákazníků, kteří jsou přítomni nebo požadují služby v daném čase, je tedy také náhodný a ovlivněn nezávislými Poissonovými procesy.
  • Nezávislé události: Poissonovo rozdělení se používá pro modelování nezávislých událostí, což znamená, že každá požadavková událost (např. poptávka nebo porucha) je nezávislá na předchozích. To znamená, že v reálných scénářích, kde jsou požadavky na služby nebo produkty náhodné a nezávislé, tento model poskytuje realistické a efektivní nástroje pro predikci a plánování.

Praktické využití

Modely se stochastickou přítomností zákazníků a Poissonovým rozdělením poptávky se široce používají v různých oblastech, kde jsou požadavky na služby nebo produkty náhodné, ale s určitou průměrnou frekvencí. Praktickými aplikacemi jsou například:

  • Údržba infrastruktury: V případě údržby elektrických vedení nebo opravy vodovodních a kanalizačních systémů může tento model pomoci optimalizovat trasy a plánování pracovních týmů, které reagují na náhodně vzniklé poruchy. Počet poruch v určité oblasti může být modelován pomocí Poissonova rozdělení, což pomáhá optimalizovat časové okna a trasování vozidel.
  • Poštovní a doručovací služby: V poštovních službách, kde je potřeba doručit zásilky na různých místech, může tento model pomoci plánovat trasy pro doručovatele, kteří se musí přizpůsobit náhodně generované poptávce. Počet požadavků na doručení může být modelován jako Poissonův proces.
  • Zdravotnické služby: V oblasti pohotovostních služeb nebo rozvozu léků může tento model pomoci efektivně plánovat trasy pro záchranné týmy nebo doručování léků, kde je počet požadavků (např. urgentních zásilek) náhodný, ale stále odpovídá Poissonově distribuci.

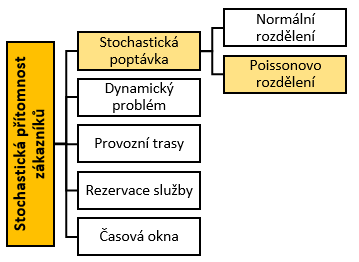
Problémy se stochastickou přítomností zákazníků a stochastickou poptávkou s Poissonovým rozdělením jsou součástí širší třídy logistických problémů, které se zabývají optimalizací tras a kapacit v prostředí, kde jsou požadavky na služby nebo produkty náhodné, ale mají známou průměrnou frekvenci. Tento model je velmi užitečný pro scénáře, jako jsou údržba infrastruktury, doručovací služby nebo pohotovostní služby, kde poptávka je modelována pomocí Poissonova rozdělení. Počet požadavků je náhodný, ale rozložení těchto událostí je pravidelné a statisticky predikovatelný, což poskytuje nástroje pro efektivní plánování a optimalizaci tras v reálných podmínkách.

Zdroj:
[1] Gendreau, M., Laporte, G., Séguin, R. (1996) Stochastic vehicle routing. European Journal of Operation Research, 88(1).
[2] Bertsimas, D. J. (1992). A vehicle routing problem with stochastic demand. Operations Research, 40(3).
[3] Oyola, J., Arntzen, H., & Woodruff, D. L. (2017). The stochastic vehicle routing problem, a literature review, part II: solution methods. EURO Journal on Transportation and Logistics, 6(4).
[4] Oyola, J., Arntzen, H., & Woodruff, D. L. (2018). The stochastic vehicle routing problem, a literature review, part I: models. EURO Journal on Transportation and Logistics, 7(3).