Manage and streamline operations across multiple locations, sales channels, and employees to has improve efficiency and your bottom line.

Problémy stochastické přítomnosti zákazníků s možností využití časových oken

Časová okna

CVRPSCD (Capacitated Vehicle Routing Problem with Stochastic Customer Demand) řeší situaci, kdy není jisté, zda zákazníci budou potřebovat obsluhu. To znamená, že trasu je nutné plánovat s ohledem na pravděpodobnost, že určitý zákazník bude aktivní. Tento problém je běžný v dodávkových a svozových službách, kde objednávky přicházejí náhodně.

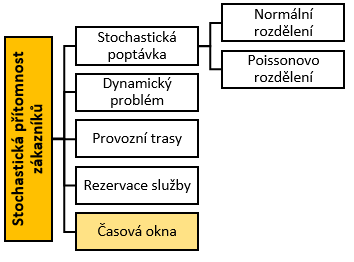
Tato varianta problému se stochastickou přítomností zákazníků přidává další faktor – časová okna, která určují, v jakém časovém rozmezí je třeba požadavky zákazníků splnit. Zákazníci mohou být přítomní náhodně, a jejich požadavky na doručení mají stanovený časový interval, ve kterém musí být doručeno zboží nebo služba. Tato varianta se zaměřuje na to, jak efektivně naplánovat trasy vozidel tak, aby nejen uspokojily poptávku, ale také dodržely časová okna stanovená zákazníky.

Zajímavost

  • Flexibilita a přesnost: Tento model ukazuje, jak kombinace stochastického chování a časových omezení může přinést výzvy v oblasti plánování a optimalizace.
  • Zajištění kvality služeb: Časová okna jsou v mnoha oblastech klíčová pro zákazníky (např. doručení balíků nebo služeb), což tento problém činí velmi praktickým.
  • Vyšší komplexnost: Tento model zvyšuje složitost oproti standardnímu VRP (Vehicle Routing Problem) tím, že musí řešit problémy s flexibilitou času a přítomnosti.

Praktické využití

  • Doručování balíků a zásilek: Když zákazníci mají specifické časové požadavky na doručení (např. doručení mezi 10:00 a 12:00), je nutné plánovat trasy, které tyto požadavky splní, i když přítomnost zákazníků je stochastická.
  • Zdravotní a servisní návštěvy: Například návštěvy lékařů, techniků nebo pracovníků údržby, kteří mají stanovená časová okna pro příchod, ale pacienti nebo zákazníci mohou být přítomní náhodně.
  • Doprava ve veřejné sféře: Například plánování tras autobusů nebo taxi služeb, kde musí být dodrženy specifické časy pro příjezdy na stanice nebo na vyzvednutí cestujících.

Problém se stochastickou přítomností zákazníků a časovými okny je praktickým a složitým přístupem k optimalizaci tras, který zohledňuje nejen náhodnou přítomnost zákazníků, ale i jejich časové požadavky. Tento model se hodí pro situace, kde je důležité nejen doručit zboží nebo služby včas, ale také flexibilně reagovat na měnící se požadavky zákazníků. Kombinace stochastické přítomnosti a časových oken představuje výzvu pro efektivní plánování, které vyžaduje vyváženost mezi flexibilitou a optimalizací.

Zdroj:
[1] Fleury, G., Lacomme, P., & Prins, C. (2004). Evolutionary algorithms for stochastic arc routing problems. In Workshops on Applications of Evolutionary Computation (pp. 501-512). Springer, Berlin, Heidelberg.
[2] Fleury, G., Lacomme, P., Prins, C., & Ramdane-Chérif, W. (2005). Improving robustness of solutions to arc routing problems. Journal of the operational research society, 56(5).
[3] Laporte, G., Musmanno, R., & Vocaturo, F. (2010). An adaptive large neighbourhood search heuristic for the capacitated arc-routing problem with stochastic demands. Transportation Science, 44(1).