Manage and streamline operations across multiple locations, sales channels, and employees to has improve efficiency and your bottom line.

Dynamický přístup v problému stochastické přítomnosti zákazníků

Tato varianta problému rozšiřuje klasický model stochastické přítomnosti zákazníků (CVRPSCD) o dynamický prvek.

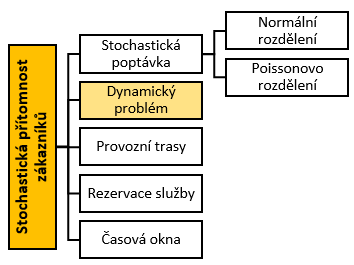
Dynamický přístup

Tato varianta problému rozšiřuje klasický model stochastické přítomnosti zákazníků (CVRPSCD) o dynamický prvek. Jak popisují Hvattum a kol. (2006), jde o situaci, kdy zákazníci neoznamují své požadavky předem, ale mohou se ozvat kdykoliv během dne. Plánování tras proto musí být flexibilní, protože některé objednávky jsou známy už předem, zatímco jiné přicházejí až po vyjetí vozidel do terénu.

Zajímavost

  • Rozhodování v reálném čase: Plánovač nebo systém musí reagovat na nové informace v průběhu dne.
  • Změny za jízdy: Vozidla mohou měnit trasu „za pochodu“ na základě nových požadavků.
  • Optimalizace v nejistotě: Systém neví, kdo se ozve a kdy, ale musí být připraven efektivně reagovat.

Praktické využití

  • Kurýrní a expresní doručovací služby, kde objednávky přicházejí v průběhu dne (např. doručení dokumentů, léků).
  • Mobilní technické služby, kdy zákazník nahlásí poruchu a tým musí být operativně nasměrován.
  • Zdravotní a sociální péče, kde může klient zavolat o pomoc náhle a je třeba flexibilně upravit trasu.

Dynamický přístup v rámci problému se stochastickou přítomností zákazníků nabízí realistické řešení pro prostředí, kde přicházejí nové požadavky v průběhu dne. Tento model je velmi praktický pro logistiku, která vyžaduje rychlé reakce a schopnost operativně měnit plán. Přístup umožňuje efektivnější využití zdrojů a lepší zákaznický servis i ve velmi proměnlivých podmínkách.

Tato varianta je typická pro kurýrní služby, svozy odpadu, rozvoz jídel nebo záchranné složky, kdy nelze dopředu s jistotou vědět, kdo požádá o službu, a vozidla musí být připravena operativně měnit trasu.

Zdroj:
[1] Fleury, G., Lacomme, P., & Prins, C. (2004). Evolutionary algorithms for stochastic arc routing problems. In Workshops on Applications of Evolutionary Computation (pp. 501-512). Springer, Berlin, Heidelberg.
[2] Fleury, G., Lacomme, P., Prins, C., & Ramdane-Chérif, W. (2005). Improving robustness of solutions to arc routing problems. Journal of the operational research society, 56(5).
[3] Laporte, G., Musmanno, R., & Vocaturo, F. (2010). An adaptive large neighbourhood search heuristic for the capacitated arc-routing problem with stochastic demands. Transportation Science, 44(1).
[4] Hvattum, L. M., Løkketangen, A., & Laporte, G. (2006). Solving a dynamic and stochastic vehicle routing problem with a sample scenario hedging heuristic. Transportation Science, 40(4).